Use our free Pythagoras Theorem Calculator to accurately compute the missing side of a right triangle based on the fundamental geometric principle a² + b² = c². Whether you know two legs and want to find the hypotenuse, or you have the hypotenuse and one leg, this tool instantly returns the correct value without any manual calculations. Ideal for students, teachers, engineers, and anyone working with geometry or spatial problems, this calculator supports quick and reliable solutions for homework, classroom exercises, and practical applications. Enter any two known side lengths of a right triangle and see the result in real time — no registration or downloads required.
Enter Two Known Sides
Triangle Diagram
Learn About Pythagoras Theorem
Test Your Knowledge
What is the Pythagoras Theorem?
The Pythagoras Theorem is a fundamental principle in geometry that describes the relationship between the three sides of a right triangle. In any right triangle (where one angle is exactly 90 degrees), the theorem states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Mathematical Formula:
Where:
• c represents the length of the hypotenuse
• a and b represent the lengths of the other two sides
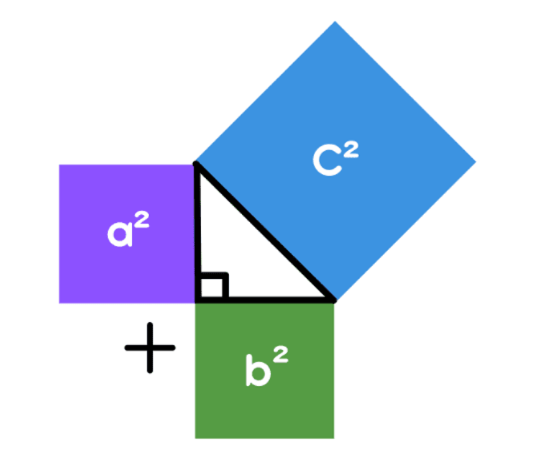
This theorem is named after the ancient Greek mathematician Pythagoras, who is credited with its discovery and proof around 500 BC. However, evidence suggests that the Babylonians and Egyptians were aware of this relationship long before Pythagoras.
Did You Know?
The Pythagorean theorem has over 400 different proofs, making it one of the most proven mathematical theorems in history. One of the most famous proofs was provided by U.S. President James Garfield in 1876!
Practical Applications
The Pythagoras Theorem has numerous real-world applications across various fields:
Construction & Architecture
Ensuring corners are perfectly square (90 degrees) and calculating diagonal measurements for buildings and structures.
Navigation & Surveying
Calculating shortest distances between points and determining positions in mapping and GPS systems.
Physics & Engineering
Resolving force vectors, calculating distances in three-dimensional space, and analyzing mechanical systems.
Computer Graphics
3D rendering, spatial calculations, and determining distances between points in virtual environments.
Real-world Example
When building a staircase, carpenters use the Pythagorean theorem to calculate the length of the stringer (the diagonal support). If the rise is 7 feet and the run is 10 feet, the stringer length would be √(7² + 10²) = √149 ≈ 12.2 feet.
Example Calculations
Finding the Hypotenuse (c)
If you know the lengths of legs a and b, you can find the hypotenuse c:
Example: If a = 3 and b = 4
Finding a Leg (a or b)
If you know the hypotenuse and one leg, you can find the other leg:
Example: If c = 10 and a = 6
Step-by-Step Triangle Calculation Example
Let's find the length of a ladder needed to reach a window 20 feet high if the base of the ladder is 15 feet from the wall:
- Identify the known values: a = 15 feet (distance from wall), b = 20 feet (height of window)
- Apply the Pythagorean theorem: c² = a² + b²
- Calculate: c² = 15² + 20² = 225 + 400 = 625
- Find the square root: c = √625 = 25 feet
- Therefore, you need a ladder at least 25 feet long
Algebraic Proofs
The Pythagoras Theorem has been proven in many ways throughout history. Here are two algebraic proofs that demonstrate the validity of the theorem:
Proof 1: Using Area Comparison
In this arrangement:
- Four identical right triangles (with legs a and b) are arranged around a central square (with side c)
- This forms a larger square with side length (a + b)
- The area of the large square = (a + b)²
- The area of the central square = c²
- The combined area of the four triangles = 4 × (½ab) = 2ab
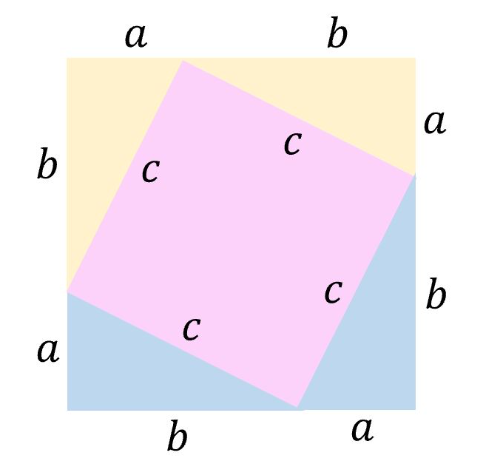
Therefore:
Proof 2: Alternative Area Comparison
In this arrangement:
- Four identical right triangles are arranged to form a larger square with side c
- The enclosed space forms a smaller square with side length (b - a)
- The area of the large square = c²
- The area of the small square = (b - a)²
- The combined area of the four triangles = 4 × (½ab) = 2ab
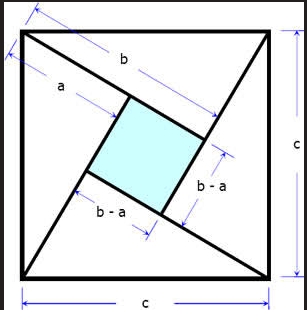
Therefore:
History of the Pythagoras Theorem
The history of the Pythagoras Theorem begins long before Pythagoras himself. Ancient Babylonian and Egyptian civilizations used the same geometric rule for measuring land and building temples as early as 1800 BC. However, it was Pythagoras of Samos, a Greek philosopher and mathematician, who first gave the theorem its logical proof and formal explanation around 500 BC.
The Pythagoreans believed that numbers explained everything in the universe, and the Pythagoras Theorem was their greatest example of mathematical perfection. Their discovery laid the foundation for geometry, algebra, and trigonometry, influencing thinkers from Euclid to Einstein.
Today, the Pythagoras Theorem remains one of the most important and widely used principles, showing that even a 2,500-year-old discovery can still power our modern world.
Frequently Asked Questions
The Pythagoras Theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This is expressed as a² + b² = c².
To find a missing side using the Pythagoras Theorem:
- If you need to find the hypotenuse (c): c = √(a² + b²)
- If you need to find a leg (a): a = √(c² - b²)
- If you need to find a leg (b): b = √(c² - a²)
Simply enter the two known values into our calculator, and it will automatically calculate the missing side for you.
No, the Pythagoras Theorem only applies to right triangles, which are triangles with one angle measuring exactly 90 degrees. For other types of triangles, you would need to use other trigonometric formulas like the Law of Cosines or the Law of Sines.
While the theorem is named after the Greek mathematician Pythagoras, who lived around 500 BC, evidence suggests that the Babylonians and Egyptians were aware of this relationship long before Pythagoras. However, Pythagoras is credited with providing the first formal proof of the theorem.
The Pythagoras Theorem has numerous real-world applications, including:
- Construction and architecture for ensuring right angles
- Navigation for calculating shortest distances
- Physics for resolving force vectors
- Computer graphics for 3D rendering
- Surveying and mapping
- Engineering and design
Tips for Using the Pythagoras Theorem
Identify the Right Angle
Always identify the right angle in the triangle first. The side opposite this angle is the hypotenuse (c), which is always the longest side.
Check Your Units
Make sure all sides are measured in the same unit before applying the theorem. If they're not, convert them to a common unit first.
Use the Correct Formula
Remember to use the correct formula based on which side you're trying to find. The formula changes slightly when finding a leg versus the hypotenuse.
Verify Your Answer
After calculating, verify your answer by plugging all three values back into the original theorem to ensure the equation holds true.
Explore Our Calculator Collection
Math Calculators
Solve complex mathematical problems with our comprehensive suite of math calculators.
Explore Math ToolsEngineering Calculators
Precision tools for engineers to solve technical problems efficiently.
Explore Engineering ToolsHealth Calculators
Monitor and improve your health with our specialized medical calculators.
Explore Health ToolsFinance Calculators
Make informed financial decisions with our comprehensive money management tools.
Explore Finance ToolsTime Calculators
Efficiently manage and calculate time with our specialized time tools.
Explore Time ToolsAt Calculator Premium, we provide accurate, easy-to-use calculators for all your needs. Our tools are designed by experts to deliver precise results with a user-friendly interface.
Browse All Calculator CategoriesRelated Geometry Tools
Triangle Area Calculator
Calculate the area of any triangle using different methods.
Calculate Triangle AreaCircle Calculator
Calculate circle properties like area, circumference, and radius.
Calculate Circle Properties